数模算法之插值与拟合

在实际问题中，往往不能直接得到一个函数$y = f(x)$的连续值，而是通过观测得到一系列离散点值。即已知函数在一个区间$[a,b]$上的一系列点值：

$$y_i = f(x_i), \quad i = 1,2,\cdots,n$$

当需要获取定义域上这些点之外的值时，常用一些函数$\varphi(x)$以代替$f(x)$，此时常用的算法有插值法和拟合法，插值函数满足通过所有已知点，而拟合函数则是在某种意义上总偏差最小。由于近似的要求不同，二者在数学方法上完全不同，在实际应用中需要根据具体情况选择。

插值法

在建模过程中，经常有这样一类数学问题：已知一些离散点，要求一条曲线将这些点连接，这就是插值问题。

以下将以此散点图为例，介绍常用的插值方法：

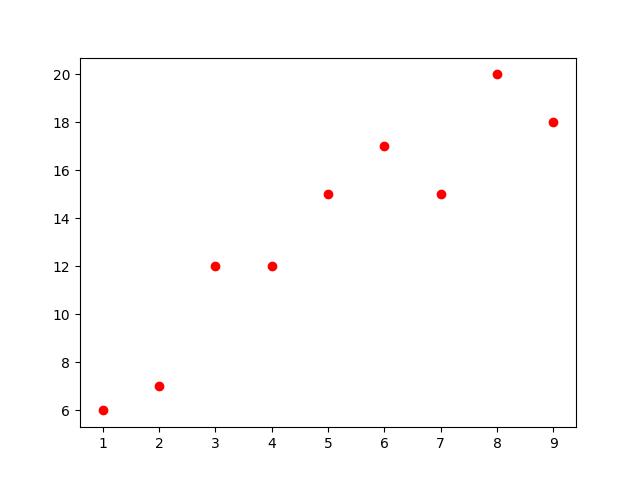
分段线性插值

分段线性插值是最简单直观的插值方法，但插值函数不连续，不适用于高精度的插值。简单的说，将相邻的两个点连接起来，如此形成的一条折线就是分段线性插值函数，记作$I_n(x)$，满足$I_n(x) = \sum y_i l_i(x)$，其中$l_i(x)$满足：

$$l_i(x) = \begin{cases} \frac{x-x_{i+1}}{x_i-x_{i+1}}, & x_i \leq x \leq x_{i+1} \\ \frac{x-x_{i-1}}{x_{i}-x_{i-1}}, & x_{i-1} \leq x \leq x_{i} \\ 0, & \text{otherwise} \end{cases}$$

（代码实现略）

如图：

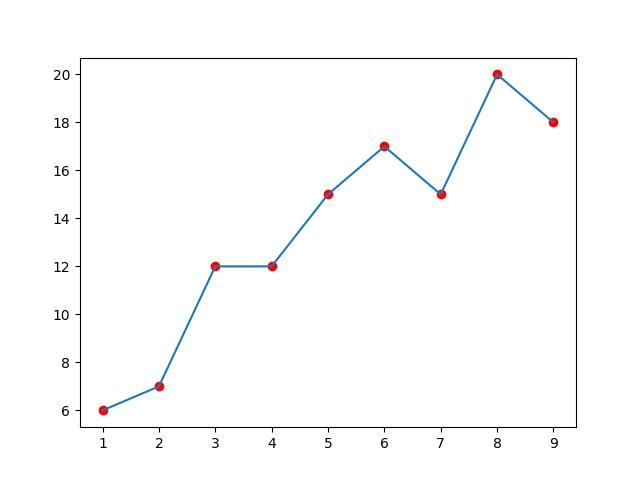
$I_n(x)$具有良好的收敛性，即$\lim\limits_{n\rightarrow+\infty}I_n(x)=f(x)$。显然$n$越大，分段越多，插值误差越小。

拉格朗日插值

拉格朗日插值的基函数为：

$$l_i(x) = \frac {(x - x_0) \dots (x - x_{i-1})(x - x_{i+1}) \dots (x - x_n)}{(x _i- x_0) \dots (x_i - x_{i-1})(x_i - x_{i+1}) \dots (x_i - x_n)}\\ = \prod_{j=0,j\neq i}^n \frac{x-x_j}{x_i-x_j}$$

拉格朗日插值函数为：

$$L_n(x) = \sum_{i=0}^n y_i l_i(x)$$

样条插值

（高考后补）