数模算法之线性规划

OIer入门数模竞赛代码手之路

在生产实践中，经常会遇到如何利用现有资源安排生成，以取得最大效益的问题。运筹学的一个重要分支——数学规划应运而生，它是一种通过数学方法来解决实际问题的方法。线性规划是数学规划的一个重要分支，它是一种在给定约束条件下，求解线性目标函数最优值的方法。

本系列偏代码向，入门之前需要了解一些基本的数学知识，如线代、微积分等。本系列（由于一些懂得都懂的原因）以Python为主，也会涉及Matlab。

线性规划问题

举个例子

某厂家生产甲乙两种产品，每件利润分别为$4000,3000$元。生产甲产品需用$A,B$两种机器加工，每件分别需要$2h,1h$；生成乙产品需用$A,B,C$三种机器加工，每件每种机器$1h$。机器每天可运行时长为$10h,8h,7h$。问如何安排生产计划，使得利润最大？

对上述问题建立数学模型：设甲乙产品的生产量分别为$x_1,x_2$时，总利润$z=4000x_1+3000x_2$最大，则：

$$\max z=4000x_1+3000x_2\\ s.t. \begin{cases} 2x_1 + x_2 \leq 10\\ x_1 + x_2 \leq 8\\ x_2 \leq 7\\ x_1 , x_2 \geq 0 \end{cases}$$

其中，$x_1,x_2$称为决策变量，函数$z=4000x_1+3000x_2$称为目标函数，s.t.标记的不等式组称为约束条件（即subject to）。由于上述目标函数与约束条件均为线性，故称线性规划。

线性规划问题的解

一般线性规划问题的（Matlab/Python）标准形式为：

$$\min z = f^T x\\ s.t.\begin{cases} A\times x \leq b\\ Aeq \times x = Beq\\ lb \leq x \leq ub \end{cases}$$

式中f,x,b,Beq,lb,ub为列向量，A,Aeq为矩阵，其中称f（也可用c表示）为价值向量，A为不等式约束矩阵，b为不等式约束向量（价值向量），Aeq为等式约束矩阵，Beq为等式约束向量，lb为下界向量，ub为上界向量。

满足约束条件的x即称为线性规划的可行解。所有可行解构成的集合称为可行域，记作$R$。其中，目标函数z最小的可行解称为最优解。

代码实现

利用Python求解线性规划问题需要导入numpy,scipy库。以上述问题为例，其数学模型转化为标准形式为：

$$\min z = -\begin{pmatrix} -4000 \\ -3000 \end{pmatrix}^T \times \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\\ s.t.\begin{cases} \begin{pmatrix} 2 & 1\\ 1 & 1\\ 0 & 1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \leq \begin{pmatrix} 10 \\ 8 \\ 7 \end{pmatrix}\\ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \geq\begin{pmatrix} 0 \\ 0 \end{pmatrix} \end{cases}$$

将参数定义为numpy矩阵后调用函数求解：

from scipy import optimize
import numpy as np

f = np.array([-4000,-3000]).transpose()
A = np.array([[2,1],[1,1],[0,1]])
b = np.array([10,8,7])

#求解
res = optimize.linprog(c=f,A_ub=A,b_ub=b,bounds=np.array([[0,None],[0,None]]))
print(res)

'''
result:
message: Optimization terminated successfully. (HiGHS Status 7: Optimal)
success: True
status: 0
fun: -26000.0
x: [ 2.000e+00  6.000e+00]
nit: 2
lower: residual: [ 2.000e+00  6.000e+00]
       marginals: [ 0.000e+00  0.000e+00]
upper: residual: [ inf inf]
       marginals: [ 0.000e+00  0.000e+00]
eqlin: residual: []
       marginals: []
ineqlin: residual: [ 0.000e+00  0.000e+00  1.000e+00]
         marginals: [-1.000e+03 -2.000e+03 -0.000e+00]
mip_node_count: 0
mip_dual_bound: 0.0
mip_gap: 0.0
'''

其中linprog的完整参数：

def linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
            bounds=None, method='interior-point', callback=None,
            options=None, x0=None)

其中：

参数	意义
c	目标函数的决策变量对应的系数向量(行列向量都可以，下同)
A_ub	不等式约束组成的决策变量系数矩阵
b_ub	由A_ub对应不等式顺序的阈值向量
A_eq	等式约束组成的决策变量系数矩阵
b_eq	由A_ub对应等式顺序的阈值向量
bounds	表示决策变量x连续的定义域的n×2维矩阵，None表示无穷
method	调用的求解方法，2.2节给出详细解释
callback	选择的回调函数
options	求解器选择的字典
x0	初始假设的决策变量向量，若可行linprog会对方法优化

求解线性规划问题的Matlab函数为：

[x,val] = linprog(f,A,b);
[x,val] = linprog(f,A,b,Aeq,Beq);
[x,val] = linprog(f,A,b,Aeq,Beq,lb,ub);

其中x为决策向量，val为此时目标函数值。

可转化为线性规划的问题

有些看起来是非线性的问题，经过转换也可以通过线性规划求解。

目标函数含绝对值

对于目标函数含绝对值的问题，可以通过引入新的变量进行转化。如：

$$\min z = |x_1|+2|x_2|+3|x_3|+4|x_4|\\ s.t.\begin{cases} x_1-x_2-x_3+x_4 \leq -2\\ x_1-x_2+x_3-3x_4 \leq -1\\ x_1-x_2-2x_3+3x_4 \leq -\frac{1}{2}\\ x_1,x_2,x_3,x_4 \geq 0 \end{cases}$$

对于绝对值问题，发现$\forall x_i,\exist u_i,v_i \geq 0:x_i=u_i-v_i,|x_i|=u_i+v_i$，只需求出$u,v$就能求出对应$x=u-v$。

因此做变量变换并将新变量排序为一维向量$y=\begin{pmatrix}u\\v\end{pmatrix}=\begin{pmatrix}u_1&...&u_4&v_1&...&v_4\end{pmatrix}$。

则上述模型转化为如下标准型：

$$\min c^T y\\ s.t.\begin{cases} \begin{pmatrix} A & -A \end{pmatrix} \times \begin{pmatrix} u \\ v \end{pmatrix}\leq b\\ u,v \geq 0 \end{cases}$$

其中：

$$c=\begin{pmatrix} 1&2&3&4&1&2&3&4 \end{pmatrix}^T\\ b=\begin{pmatrix} -2&-1&-\frac{1}{2} \end{pmatrix}^T\\ A = \begin{pmatrix} 1&-1&-1&1\\ 1&-1&1&-3\\ 1&-1&-2&3 \end{pmatrix}$$

然后调用linprog函数求解即可：

from scipy import optimize
import numpy as np

c = np.array([1,2,3,4,1,2,3,4]).transpose()
A = np.array([[1,-1,-1,1],[1,-1,1,-3],[1,-1,-2,3]])
b = np.array([-2,-1,-1/2])

res = optimize.linprog(c=f,A_ub=np.hstack((A,-A)),b_ub=b,bounds=np.array([[0,None]]*8))
print(res)

目标函数含最值

如求解$\min\limits_{x_i}\{\max\limits_{y_i}|x_i-y_i|\}$，可以取$z = \max\limits_{y_i}|x_i-y_i|$。

以上问题则转化为：

$$\min z\\ s.t.\begin{cases} x_i-y_i \leq z\\ y_i-x_i \leq z \end{cases}$$

即可使用一般线性规划求解。

常见模型之投资的收益与风险

问题描述

市场上有$n$种资产$s_i(i=1,2,…,n)$可以选择，现用数额为M的相当大的资金作一个时期的投资。这$n$种资产在这一时期内购买$s_i$的平均收益率为$r_i$，风险损失率为$q_i$,投资越分散，总风险越少，总体风险可用投资的$s_i$中最大的一个风险来度量。

购买$s_i$时要付交易费，费率为$p_i$,当购买额不超过给定值$u_i$时，交易费按购买$u_i$计算。另，假定同期银行存款利率是$r_0$，既无交易费又无风险$(r_0=5\%)$。

投资的相关数据$(n=4)$：

$s_i$	$r_i/\%$	$q_i/\%$	$p_i/\%$	$u_i/\text{rmb}$
$s_1$	28	2.5	1	103
$s_2$	21	1.5	2	198
$s_3$	23	5.5	4.5	52
$s_4$	25	2.6	6.5	40

符号规定与基本假设

• 符号规定
  • $s_i$代表第$i$种投资项目，特别地，$s_0$代表存入银行；
  • $p_0=q_0=0$；
  • $x_i$表示投入$s_i$的资金；
  • $a$代表投资风险度；
  • $Q$代表总体收益。
• 基本假设
  • 投资数额$M$相当大，且远大于$u_i$；（部分特殊模型可能不成立，可以通过更改bounds参数处理）；
  • $s_i$之间相互独立；
  • 投资期间$r_i,p_i,q_i$保持不变；
  • $a,Q$只受$r_i,p_i,q_i$影响。

模型分析与建立

总体风险

按照题意，总体风险可用投资的$s_i$中最大的一个风险来度量，即：

$$\max q_ix_i$$

总体收益

总体收益为各项投资的收益之和减去投资手续费之和，其中手续费为分段函数：

$$p = \begin{cases} p_iu_i & x_i \leq u_i\\ p_ix_i & x_i > u_i \end{cases}$$

由基本假设可知，$M>>p_iu_i$，故可假设$x_i > u_i$恒成立，则总体收益为：

$$Q = \sum(r_i-p_i)x_i$$

建立模型

要使收益尽可能大，风险尽可能小，需要建立一个多目标线性规划模型：

$$\begin{cases} \max \sum(r_i-p_i)x_i\\ \min \max q_ix_i \end{cases}\\ s.t.\begin{cases} \sum (1+p_i)x_i = M\\ x_i \geq 0 \end{cases}$$

模型简化

在实际投资中，不同公司侧重点不同，有的公司更看重风险，有的公司更看重收益。因此有以下三种简化方式：

固定风险水平，最大化收益

给定一个风险上限$a$，令总体风险不超过$a$的情况下，即$\frac{q_ix_i}{M}\leq a$，使收益最大化，则模型可转化为如下单目标线性规划：

$$\max \sum(r_i-p_i)x_i\\ s.t.\begin{cases} \frac{q_ix_i}{M}\leq a\\ \sum (1+p_i)x_i = M\\ x_i \geq 0 \end{cases}$$

固定收益水平，最小化风险

给定一个收益下限$k$，使风险最小化：

$$\min \max q_ix_i\\ s.t.\begin{cases} \sum (1+p_i)x_i = M\\ \sum(r_i-p_i)x_i \geq k\\ x_i \geq 0 \end{cases}$$

分别赋予权重

引入投资偏好系数$s\in (0,1]$，对风险和收益分别赋予权重$s$和$1-s$：

$$\min \{s*\max q_ix_i-(1-s)*\sum(r_i-p_i)x_i\}\\ s.t.\begin{cases} \sum (1+p_i)x_i = M\\ x_i \geq 0 \end{cases}$$

代码实现（以模型一为例）

由于不同投资者有不同的风险度，故对风险度$a$进行循环搜索并绘制图像：

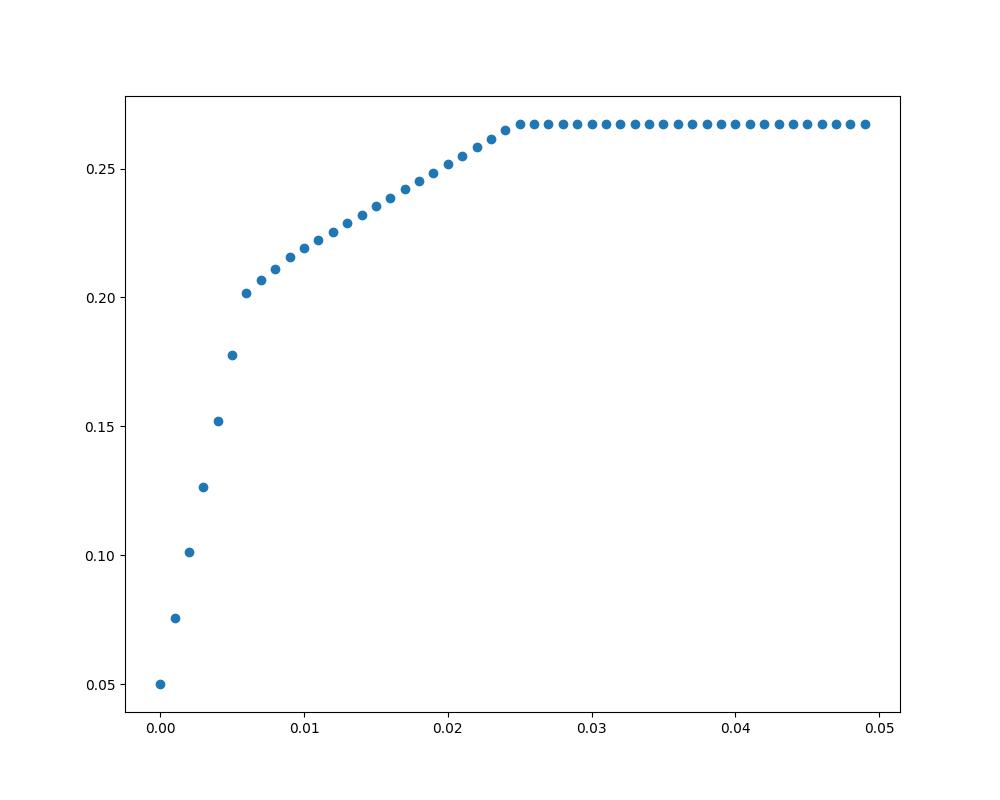
from scipy import optimize
import numpy as np
import matplotlib.pyplot as plt

a = 0
c = np.array([-0.05,-0.27,-0.19,-0.185,-0.185]).transpose()
A = np.array([
    [0,0,0,0,0],
    [0,0.025,0,0,0],
    [0,0,0.015,0,0],
    [0,0,0,0.055,0],
    [0,0,0,0,0.026]
])
Aeq = np.array([[1,1.01,1.02,1.045,1.065]])
beq = np.array([1])
bounds = np.array([[0,None]]*5)

x = []
y = []

while a<0.05:
    b = np.array([[a]]*5)
    res = optimize.linprog(c=c, A_ub=A, b_ub=b, A_eq=Aeq, b_eq=beq, bounds=bounds)
    x.append(a)
    y.append(-res.fun)
    a += 0.001

plt.figure(figsize=(10, 8),dpi=100)
plt.scatter(x,y)
plt.show()
plt.savefig('./figure.jpg')

结果分析：

• 风险大，收益也大
• 投资分散时风险较小
• 对并无偏好的投资者应选择曲线转折点投资，以达到最优效果